Question

Water coming out from a fountain is modeled by the function f(x) = −x2 + 8x + 2 where f(x) represents the height, in feet, of the water from the fountain at different times x, in seconds.What does the average rate of change of f(x) from x = 1 to x = 4 represent?

Answer 1

If f(x)represents the height, then the rate of change of f(x) would be the change in height over time. Therefore, the average rate of change would represent the change in height of the water between f(4) and f(1)

Answer 2

The average rate of change of f(x) form x =1 to x=4 is 3 and it represent that on average every unit of time between 1 and 4, the height of the fountain change 3 feets.

Explanation:

the function f(x) represent the height of the water from the fountain at different times. With this equation we can calculate the difference height at time x=1 and a time x=4.

1. For x=1

Replacing x by 1 on the function f(x)=-x^2+8x+2:

f(1) = -(1)^2 + 8(1) + 2

f(1) = -1 + 8 + 2 = 9

The height of the water at 1 unit of time is 9 feets.

2. For x=4

Replacing x by 1 on the function f(x)=-x^2+8x+2:

f(4) = -(4)^2 + 8(4) + 2

f(1) = -16 + 32 + 2 = 18

The height of the water at 4 unit of time is 18 feets.

In general, the average rate of change f(x) from x=a to x=b is expressed by:

`(f(b) - f(a) )/( b - a )`

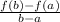
So, the average rate of change of f(x) from x=1 to x=4 is calculate as:

`(f(4) - f(1) )/( 4 - 1 )`

=
`(18 feets- 9 feets )/( 4 unit of time - 1 unit of time)`

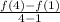
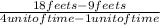
= 3 feets /unit of time

Taking into account the units obtain from the equation above, the average rate of change is saying that between 1 to 4 units of time, every unit of time the height of the water changed 3 feets.