Question

The​ sales, s, of a product have declined in recent years. there were 201 million sold in 1984 and 1.3 million sold in 1994. assume the sales are decreasing according to the exponential decay​ model, upper s left parenthesis t right parenthesis equals upper s 0 e superscript negative kt baseline . ​a) find the value k and write an exponential function that describes the number sold after​ time, t, in years since 1984. ​b) estimate the sales of the product in the year 2002. ​c) in what year​ (theoretically) will only 1 of the product be​ sold?

Answer 1

the correct answer is A)

Answer 2

a) find the value k and write an exponential function that describes the number sold after​ time, t, in years since 1984.

For this case we have an equation of the form:

`image`

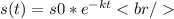
From here, we must find the values of s0 and k.

For this, we use the following data:

There were 201 million sold in 1984 and 1.3 million sold in 1994.

Therefore, the initial sales are:

`image`

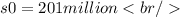
Then, the value of k is given by:

`1,300,000 = 201,000,000e ^ {-10k}`

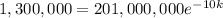
Clearing k we have:

`image`

`image`

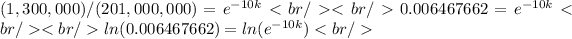
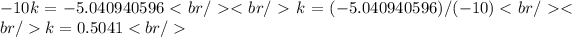
Thus, the generic equation is:

`image`

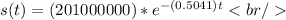
b) estimate the sales of the product in the year 2002

For the year 2002 we have:

`image`

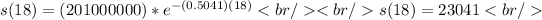
c) in what year​ (theoretically) will only 1 of the product be​ sold?

By the time 1 single product is sold, we have:

`image`

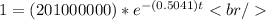
Clearing the time we have:

`image`

`image`

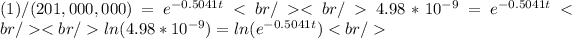
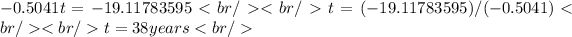
Therefore, only 1 product will be sold after 38 years.