The "explanation" for the problem has a typo in it. There are 11 possible ice cream/yogurt flavors to choose from, regardless of whether any are low-fat, so the total number of ways of choosing any 2 from the selection is
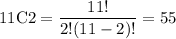
In particular we want to count the number of ways of picking 1 ice cream and 1 yogurt flavor from the low-fat variety. There are 6 total choices that are not low-fat of which we choose 0, 3 choices of low-fat ice cream of which we choose 1, and 2 choices of low-fat yogurt of which we also choose 1. In terms of the binomial coefficient, this is

So the probability of getting such a combination is

.