Question

Find the area of the parallelogram with vertices k(1, 1, 1), l(1, 3, 2), m(5, 8, 2), and n(5, 6, 1).

Answer 1

The area can be found as the magnitude of the cross product of the vectors representing two adjacent sides.
area = || kl × kn || = || (0, 2, 1) × (4, 5, 0) ||
= || (-5, 4, -8) || = √105


_____
For the purpose here, kl = l - k = (1, 3, 2) - (1, 1, 1) = (0, 2, 1)
and nk = n - k = (5, 6, 1) - (1, 1, 1) = (4, 5, 0)

The cross product can be calculated using a suitable calculator. By hand, it is the determinant

`\left|\begin{array}{ccc}i&j&k\\0&2&1\\4&5&0\end{array}\right|`
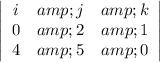
where i, j, k are unit vectors in the x, y, z directions.