Question

1. Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay.

f(x) = 7.2 ⋅ 1.08^x
a. Exponential growth function; 8%
b. Exponential decay function; 108%
c. Exponential growth function; 108%
d. Exponential growth function; 0.08%

2. Decide whether the function is an exponential growth or exponential decay function, and find the constant percentage rate of growth or decay.
f(x) = 2034 ⋅ 0.9939^x
a Exponential growth function; 0.0061%
b Exponential decay function; -0.61%
c Exponential growth function; -0.61%
d Exponential decay function; 0.0061%

3. Find the exponential function that satisfies the given conditions:
Initial value = 30, increasing at a rate of 13% per year
a f(t) = 30 ⋅ 1.13t
b f(t) = 13 ⋅ 1.13t
c f(t) = 30 ⋅ 0.13t
d f(t) = 30 ⋅ 13t

4. Find the exponential function that satisfies the given conditions:
Initial value = 70, decreasing at a rate of 0.5% per week
a f(t) = 0.5 ⋅ 0.3t
b f(t) = 70 ⋅ 1.005t
c f(t) = 70 ⋅ 0.995t
d f(t) = 70 ⋅ 1.5t

Answer 1

1. The correct option is a.

2. The correct option is b.

3. The correct option is a.

4. The correct option is c.

Explanation:

A general exponential function is defined as

`f(x)=a(b)^x`

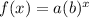
It can also written as

`f(x)=a(1+r)^x` (For growth) or
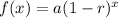`f(x)=a(1-r)^x` (For decay)

where, a is initial value, b is growth factor.

If 0<b<1, then f(x) is a decay function, if b>1, the f(x) is growth function.

(1).

The given function is

`f(x)=7.2\cdot 1.08^x`

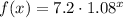
Here, the initial value is 7.2 and growth factor is 1.08.

Growth factor is greater than 1, so f(x) is exponential growth function and percentage rate of growth is

`r=1.08-1=0.08=8\%`

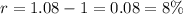
Therefore the correct option is a.

(2)

The given function is

`f(x)=2034\cdot 0.9939^x`

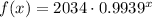
Here, the initial value is 2034 and growth factor is 0.9939.

Growth factor is less than 1, so f(x) is exponential decay function and percentage rate of growth is

`r=0.9939-1=-0.0061=-0.61\%`

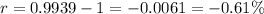
Therefore the correct option is b.

(3)

Initial value = 30, increasing at a rate of 13% per year

a=30, r=0.13.

The required function is

`f(x)=a(1+r)^t`

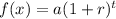
Substitute a=30 and r=0.13.

`f(x)=30(1+0.13)^t`

`f(x)=30(1.13)^t`

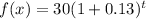
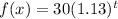
Therefore the correct option is a.

(4)

Initial value = 70, decreasing at a rate of 0.5% per week

a=70, r=0.005

The required function is

`f(x)=a(1-r)^t`

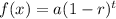
Substitute a=70 and r=0.005.

`f(x)=70(1-0.005)^t`

`f(x)=70(0.995)^t`

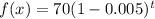
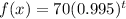
Therefore the correct option is c.