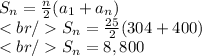First we will find the number of integers between 301 and 400 that are multiples of 4. We can see that the first such number is 304 being a multiple of 4. So the required numbers are 304, 308, 312,...,400 which form an AP.
To find the number of such integers use,
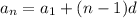 . Here
. Here
 is the nth term,
is the nth term,
 is the common difference of the AP. Here its is
is the common difference of the AP. Here its is
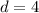 . So
. So

The required sum of the AP is