Answer: The given function is a polynomial function with leading coefficient -2.
Step-by-step explanation: We are given to determine whether the following function is a polynomial function :
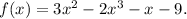
If yes, we are to state the degree and the leading coefficient. If not, we are to state the reason.
We know that
any polynomial function is of the form :
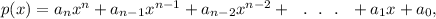
with degree n.
Son according to this definition, the given function f(x) is a polynomial function with degree 3.
The standard form of the given polynomial function is:
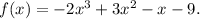
Since the leading coefficient is the coefficient of the highest power of x, so the leading coefficient is -2.
Thus, the given function is a polynomial function with leading coefficient -2.