Question

From a window 20 feet above the ground, the angle of elevation to the top of a building across the street is 78°, and the angle of depression to the base of the same building is 15°. find the height of the building across the street.\

Answer 1

The answer would be 371.16 ft.

Refer to the diagram for the scenario. The drawing is not to scale.

Notice the diagram that you will find to adjacent right triangles. All you need to do is first solve for the needed side of one triangle, by using one side.

It sounds confusing I know, but let's do this step by step.

Angle of depression is 15°.

We use this first because we do not have enough data to use the angle of elevation.

To get the adjacent side, we use the trigonometric function TOA which means:

`tan\theta= (opposite)/(adjacent)`

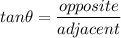
We use the height of the first building as our reference, so our given will be:

Opposite = 20ft

θ = 15°

Now we put that into our formula:

`tan\theta= (opposite)/(adjacent)`

`Tan15 = (20ft)/(adjacent)`

`adjacent = (20ft)/(Tan15)`

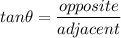
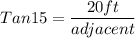
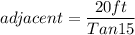
Adjacent = 74.64 ft

Angle of elevation is 78°:

Now that we have that we can solve for the height from the point of 20ft. We use the same formula, because we are looking for the opposite, given the adjacent.

`tan\theta= (opposite)/(adjacent)`

`Tan78 = (opposite)/(74.64ft)`

`(74.64ft)(Tan78) = opposite`

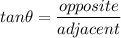
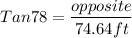
351.16ft = Opposite

Now that's the height from the top of the first building. To get the total height of the building we just add the 20ft.

351.16ft + 20 ft = 371.16ft

The building across the street is 371.16 ft tall.