Question

What is the length of AC?

Answer 1

I think it is  C not sure if i'm correct though

Answer 2

C. 126

Explanation:

We have been given a diagram. We are asked to find the length of AC.

We can see that triangle CDE is similar to triangle CBA.

We know that corresponding sides of similar triangles are proportional, so we can set an equation as:

`(140-x)/(x)=(81)/(9)`

`(140-x)/(x)*x=(81)/(9)*x`

`140-x=9x`

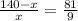
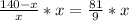
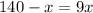
Switch sides:

`9x=140-x`

`9x+x=140-x+x`

`10x=140`

`(10x)/(10)=(140)/(10)`

`x=14`

`\overline{AC}=140-x`

`\overline{AC}=140-14`

`\overline{AC}=126`

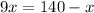
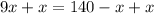
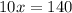
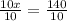
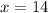
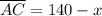
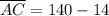
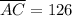
Therefore, the length of line segment is 126 and option C is the correct choice.