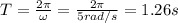Question

A 100g mass is attached to a spring and undergoes simple harmonic motion. its maximum acceleration is 15 m/s2 and its maximum speed is 3 m/s. the period of the motions is given by

Answer 1

In a simple harmonic motion, the maximum speed is given by:

`v_(max)=\omega A`

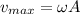
where
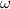`\omega` is the angular frequency and A is the amplitude of the motion, while the maximum acceleration is given by

`a_(max)=\omega^2 A`

The problem tells us both the values of the maximum speed,
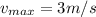`v_(max)=3 m/s`, and the maximum acceleration,
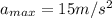`a_(max)=15 m/s^2`, so we can write the following equations:

`\omega A=3`

`\omega^2 A=15`

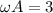
and the solutions are
`\omega=5 rad/s`,
`A=(3)/(5)m`.

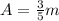We are only interested in the angular frequency; in fact, we can find the period of the motion by using the equation:

`T=(2 \pi)/(\omega)=(2 \pi)/(5 rad/s)=1.26 s`