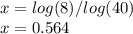Question

Which of the following is equivalent to log408 rounded to three decimal places?

0.399

0.498

0.564

1.774

Answer 1

0.564

Explanation:

Just took the test

Answer 2

The answer is:
`0.564`

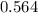
The explanation is shown below:

1. To solve this problem you must apply the following proccedure:

2. You have the logarithm expression:

`log40(8)=x`

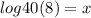
3. First, you must apply the following property:

`a^(loga(x)) =x`

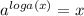
4. Therefore, you have:

`40^(log40(8))=40^(x) \\ 8=40^(x)`

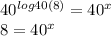
5. By applying logarithm on both sides, you have:

`log(8)=log(40^(x) )`

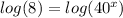
6. By applying the property
`log(a)^(b) =blog(a)`:

`image`

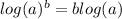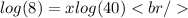
7. Solve for x:

`x=log(8)/log(40)\\ x=0.564`