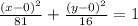Question

Write an equation in standard form of an ellipse that is 8 units high and 18 units wide. The center of the ellipse is (0,0)

Answer 1

check the picture below.


`\bf \begin{cases} h=0\\ k=0\\ a=9\\ b=4 \end{cases}\implies \cfrac{(x-0)^2}{9^2}+\cfrac{(y-0)^2}{4^2}=1\implies \cfrac{x^2}{81}+\cfrac{y^2}{16}=1`

Answer 2

Equation of Ellipse in standard form is
`((x-0)^2)/(81)+((y-0)^2)/(16)=1`

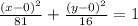
Explanation:

Given: Center of ellipse is ( 0 , 0 )

Ellipse is 8 units high.

⇒ Length of minor axis = 8

⇒ b =
`(8)/(2)=4`

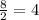
Ellipse is 18 units wide.

⇒ Length of minor axis = 18

⇒ a =
`(18)/(2)=9`

Standard equation of ellipse whose major axis ia x-axis is given by,

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

where ( h , k ) is coordinates of center.

⇒ Equation of Ellipse :
`((x-0)^2)/(9^2)+((y-0)^2)/(4^2)=1`

`(x^2)/(81)+(y^2)/(16)=1`

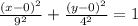
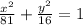
Therefore, Equation of Ellipse in standard form is
`((x-0)^2)/(81)+((y-0)^2)/(16)=1`