Question

Solve: 5-3|2x-5| ≤-1

Answer 1

`\sf \large \: x≥ (7)/(2) or x≤ (3)/(2)`

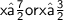
Explanation:

Let's solve your inequality step-by-step.

5−3(|2x−5|)≤−1

−3(|2x−5|)+5≤−1

Step 1: Add -5 to both sides.

−3(|2x−5|)+5+−5≤−1+−5

−3(|2x−5|)≤−6

Step 2: Divide both sides by -3.

−3(|2x−5|)/−3 ≤ −6/−3

|2x−5|≥2

Step 3: Solve Absolute Value.

|2x−5|≥2

We know either2x−5≥2or2x−5≤−2

2x−5≥2(Possibility 1)

2x−5+5≥2+5(Add 5 to both sides)

2x≥7

2x/2 ≥ 7/2

(Divide both sides by 2)

x≥7/2

2x−5≤−2(Possibility 2)

2x−5+5≤−2+5(Add 5 to both sides)

2x≤3

2x/2 ≤ 3/2

(Divide both sides by 2)

x≤ 3/2