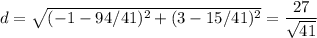We could use the formula, derive the formula, or just work it out for this case. Let's do the latter.
The distance of a point to a line is the length of the perpendicular from the line to the point.
So we need the perpendicular to 5x-4y=10 through (-1,3). To get the perpendicular family we swap x and y coefficients, negating one. We get the constant straightforwardly from the point we're going through:
4x + 5y = 4(-1)+5(3) = 11
Those lines meet at the foot of the perpendicular, which is what we're after.
4x + 5y = 11
5 x - 4y = 10
We eliminate y by multiplying the first by four, the second by five and adding.
16x + 20y = 44
25x - 20y = 50
41x = 94
x = 94/41
y = (11 - 4x)/5 = 15/41
We want the distance from (-1,3) to (94/41,15/41)