Imagine right triangle with first leg to be the Chad length and second leg to be the Chad's shadow. Second leg has length 14.3 ft and since t
he straight-line distance from the top of Chad’s head to the end of the shadow creates a 23° angle with the ground, you could consider the trigonmetric function
 ,
,
then
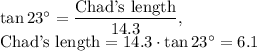 .
.