Question

Two cylinders are similar. The radius of cylinder A is 5.6 inches. The radius of cylinder B is 1.4 inches. If the height of cylinder B is 4 inches, what is the height of cylinder A? 8.2 inches 8.2 square inches 16 inches 16 square inches

Answer 1

C. 16 inches is correct

Explanation:

We are given the dimensions of the cylinders as,

Cylinder A: Radius = 5.6 inches and Height = x inches

Cylinder B: Radius = 1.4 inches and Height = 4 inches

Now, as the cylinders are similar, the ratio of the measurements will be equal.

So, we get,

`(R_(A))/(R_(B))=(H_(A))/(H_(B))`

i.e.
`x=(5.6* 4)/(1.4)`

i.e.
`x=(22.4)/(1.4)`

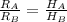
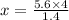
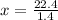
i.e. x = 16

Thus, the height of the cylinder A is 16 inches.

Hence, option C is correct.

Answer 2

If two cylinders are similar, then all their linear measurements have equal ratios. Hence:

`(r_A)/(r_B) =(h_A)/(h_B)`.

Since the radius of cylinder A is 5.6 inches, the radius of cylinder B is 1.4 inches and the height of cylinder B is 4 inches, you can find the height of cylinder A:

`(5.6)/(1.4) =(h_A)/(4)`.

Use the cross multiplication:

`1.4h_A=5.6\cdot 4,\\ 1.4h_A=22.4,\\ h_A=(22.4)/(1.4) =16` in.

Answer: the height of cylinder A 16 inches.