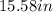Question

The base of a solid oblique pyramid is an equilateral triangle with a base edge length of 18 inches.What is the height of the triangular base of the pyramid?

Answer 1

To solve this problem you must apply the proccedure shown below:

By definition, an equilateral triangle has equal sides and all its internal angles are
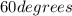`60 degrees`. If you divide it into two right triangles, you can apply the Pythagorean Theorem to calculate the height of the triangular base of the pyramid, as following:

`h=\sqrt{18in^(2)-9in^(2)}\\ h=15.58in`

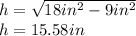
Therefore, as you can see, the answer is:
`15.58in`

Answer 2

The task is, in fact, to find the height of the equilateral triangle with a base edge ob 18 inches. Let ΔABC be the base with AB=BC=CA=18 in. Let AD be an altitude perpendicular to the side BC. Consider the triangle ADB, it is right triangle with hypotenuse AB=18 in., leg DB=18÷2=9 in. and AD unknown leg. By the Pythagorean theorem:

`AB^2=BD^2+AD^2,\\ AD^2=18^2-9^2,\\ AD^2=324-81=243,\\ AD=√(243) ,\\ AD=9√(3)`

Answer: the height of the triangular base of the pyramid is
`9√(3)`.