Question

Distance between parallel lines y=3x+10 and y=3x-20

Answer 1

1. Take an arbitrary point that lies on the first line y=3x+10. Let x=0, then y=10 and point has coordinates (0,10).

2. Use formula
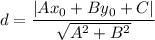`d=(|Ax_0+By_0+C|)/(√(A^2+B^2))` to find the distance from point
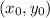`(x_0,y_0)` to the line Ax+By+C=0.

The second line has equation y=3x-20, that is 3x-y-20=0. By the previous formula the distance from the point (0,10) to the line 3x-y-20=0 is:

`d=(|3\cdot 0-10-20|)/(√(3^2+(-1)^2))=(30)/(√(10))=3√(10)`.

3. Since lines y=3x+10 and y=3x-20 are parallel, then the distance between these lines are the same as the distance from an arbitrary point from the first line to the second line.

Answer:
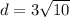`d=3√(10)`.