Question

I need help pleaseeee

Answer 1

A)

the unit price will be $5.75/(area in in²), bearing in mind that since the diameter is 10, its radius is 5.


`\bf \stackrel{area}{\pi 5^2\implies 25\pi }\qquad \qquad \stackrel{\textit{unit price}}{\cfrac{5.75}{25\pi }}\quad \approx \quad 0.73~(\$)/(in^2)`



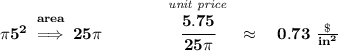
B)

well, the 16-inch pizza has 8 slices, if it were to be sold by $2 per slice, the price will not be 12.75, but 16 bucks. Well, 16 - 12.75 is a 3.25 profit.

if we take 12.75 to be the 100%, what is 3.25 off of it in percentage?


`\bf \begin{array}{ccll} amount&\%\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ 12.75&100\\ 3.25&x \end{array}\implies \cfrac{12.75}{3.25}=\cfrac{100}{x} \\\\\\ x=\cfrac{3.25\cdot 100}{12.75}\implies x\approx 25.49\implies \stackrel{rounded~up}{x\approx 25.5}`



C)

first off, we know the personal pizza has a radius of 5 inches, so it has an area of πr², or 25π, which is roughly 78.54.

what's the area of a tray with that circumference?


`\bf \stackrel{circumference}{C=2\pi r }\qquad 32=2\pi r\implies \cfrac{32}{2\pi }=r\implies \boxed{\cfrac{16}{\pi }=r} \\\\\\ \stackrel{area}{A=\pi r^2}\implies A=\pi \left( \boxed{\cfrac{16}{\pi }} \right)^2\implies A=\pi \cdot \cfrac{16^2}{\pi^2 } \\\\\\ A=\cfrac{256}{\pi }\implies A\approx 81.49\impliedby \textit{is large enough to hold 78.54 }in^2`



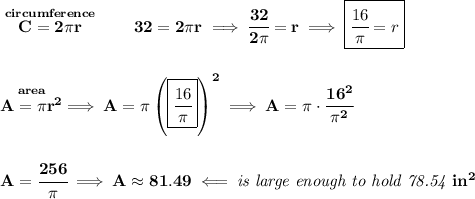
D)

well, the radius of the large pizza is 9 inches, and the radius of the small pizza is 8 inches, so their respective areas are 81π and 64π.

is 81π - 64π equals to 2? well, you already know that one.