Question

Can someone please help me on this algebra 2 question

Answer 1

Hello!

First of all, we will need to find the slope of the line using the following equation.


`( y_(2) - y_(1) )/( x_(2)- x_(1) )`

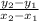
The numbers next to the variables just represent what ordered pair the number is coming from. You can switch the ones and twos and the slope will be the same. We will have (-10,7) represent (
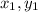
`x_(1) , y_(1)`) and (5,4) represent (
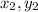
`x_(2) , y_(2)`) Now we will plug these values into the equation.


`(4-7)/(5+10) = -(3)/(15) = -(1)/(5)`

Our slope is -1/5.
---------------------------------------------------------------------
Now that we have our slope we need to find the y-intercept so we can write the equation. To do so we will put the information we have in slope intercept form, and substitute x and y with an ordered pair from the graph. Then we will solve for b. We will use the point (5,4)

4=
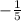
`- (1)/(5)`(5)+b
4=-1+b
b=5

Now we can put our final answer in slope intercept form.

y=-1/5x+5

I hope this helps!

Answer 2

There are two ways to figure out which of the equations goes through the point. We can either substitute the values of the point in for x and y in every single equation, or, we can do the easier way (at least in this scenario). Since all of these equations have different slopes, it would be best to find the slope of the line that goes through the points (-10,7) and (5,4). Slope is rise over run, and in this case, it simplifies to:


`(7-4)/(-10-5)`=
=
`(3)/(-15)`
=
`(-1)/(5)`

Now we can look through the equations and see which of them has a slope of
`(-1)/(5)`, and we see that it is the first one.