Question

PLEASE ANSWER QUICK 25 ACTUAL POINTS!

Find the standard form of the equation of the parabola with a vertex at the origin and a focus at (0, -7).


(Answer choices are in picture)

Answer 1

Formula for parabola with focus at (0,p) and vertex at origin
`y^2 = 4px`

Since focus is at (0,-7), p = -7 and
`y^2 = -28x`

Answer 2

The vertex of the parabola is at (0,0), and the focus is at (0,-7).

The focus is given by the following values:


`(h, k + p)`

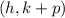
h and k represent the x and y values of the vertex. We want to solve for p.

Set the y value for the focus equal to -7:


`k + p = -7`

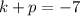
We know that k = 0, so we can simplify to get p by itself:


`p = -7`

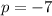
Standard form of a vertical parabola is given by the following formula:


`(y - k)^2 = 4p(x - h)`

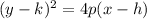
Plug in all of your known values into the formula:


`h = 0, k = 0, p = -7`


`(y - 0)^2 = 4(-7)(x - 0)`

`y^2 = -28x`

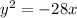
The answer is "y^2 = -28x".