Question

Graph each of the equations and then determine which one represents the rank catcher that is elevated

Answer 1

We have two functions that are Parabolas. A parabola is a type of quadratic function which is a special type of “U”-shaped curve called. So let's solve this problem for the first parabola and then for the second one.

1. Graph of the first equation

We have that:


`y=x^2-2x+3`

So if we graph this equation, the parabola that matches it is shown in Figure 1.

1.1 Direction of Parabola

In general, a parabola or quadratic function is given by the following way:


`y=ax^2+bx+c \\ \\ where \`

Given that our leading coefficient is positive, then the direction of the parabola is upward, that is, it opens upward.

1.2 Location of vertex with respect to the x-axis

The vertex a parabola can be found as follows:


`(-(b)/(2a),f(-(b)/(2a)))`


`But: \\ \\ a=1 \\ b=-2 \\ c=3 \\ \\ Accordingly: \\ \\ -(b)/(2a)=-((-2))/(2(1))=1 \\ \\ f(1)=1^2-2(1)+3=2 \\ \\ So \ the \ vertex \ is: \\ \\ V(1,2)`

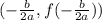
So the vertex is located two units above the x-axis.

1.3 Determine if the graph depicts the rain gauge

A rain gauge is an instrument used by meteorologists and hydrologists to gather and measure the amount of liquid precipitation over a set period of time.

From Figure 4 we can affirm that this is the parabola that resembles a rain gauge elevated from the ground.

1.4 Why or why not?

It basically the question asks for the parabola that has a vertex well above the x-axis. From Figure 4, you can see that the elevated parabola is in fact:


`y=x^2-2x+3`

2. Graph of the second equation

We have that:


`y=x^2+4x+4`

So if we graph this equation, the parabola that matches it is shown in Figure 2.

2.1 Direction of Parabola

As in the previous problem, given that our leading coefficient is positive, then the direction of the parabola is also upward, that is, it opens upward.

2.2 Location of vertex with respect to the x-axis

The vertex of a parabola can be found as follows:


`(-(b)/(2a),f(-(b)/(2a)))`


`In \ this \ case: \\ \\ a=1 \\ b=4 \\ c=3 \\ \\ Accordingly: \\ \\ -(b)/(2a)=-(4)/(2(1))=-2 \\ \\ f(-2)=(-2)^2+4(-2)+4=0 \\ \\ So \ the \ vertex \ is: \\ \\ V(-2,0)`

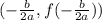
So the vertex lies on the x-axis.

2.3 Determine if the graph depicts the rain gauge

This parabola does not resembles a rain gauge elevated from the ground.

2.4 Why or why not?

As you can see the parabola touches the x-axis. If the x-axis represents the ground, then the rain gauge is touching it, that is, it is not elevated.

3. Graph of the third equation

We have that:


`y=3x^2+21x+30`

So if we graph this equation, the parabola that matches it is shown in Figure 5.

3.1 Direction of Parabola

As in the previous parabolas, given that our leading coefficient is positive, then the direction of the parabola is also upward, that is, it opens upward.

3.2 Location of vertex with respect to the x-axis


`In \ this \ case: \\ \\ a=3 \\ b=21 \\ c=30 \\ \\ Accordingly: \\ \\ -(b)/(2a)=-(21)/(2(3))=-(7)/(2) \\ \\ f(-(7)/(2))=3(-(7)/(2))^2+21(-(7)/(2))+30=-(27)/(4) \\ \\ So \ the \ vertex \ is: \\ \\ V(-(7)/(2),-(27)/(4))`

So the vertex is shifted
`(27)/(4)` units downward the x-axis.

3.3 Determine if the graph depicts the rain gauge

This parabola does not resembles a rain gauge elevated from the ground.

3.4 Why or why not?

The vertex of this parabola lies on the negative y-axis. So it is not elevated from the ground.