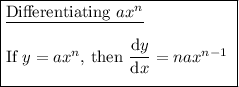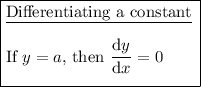Question

The cubic function p(x) = ax^3 + bx^2 + cx + d has a tangent equation y = 3x + 1 at the point (0, 1) and has a turning point at (-1, -3). Find the values of a, b, c and d. ( Show all ways of solving this math) btw the answer is a = -5, b = -6, c = 3, d = 1. show me the clearest workout

Answer 1

`p(x) = -5x^3 -6x^2 + 3x + 1`

Explanation:

Given cubic function:

`p(x) = ax^3 + bx^2 + cx + d`

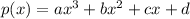
As point (0, 1) is on the curve, substitute x = 0 into the function, set it to 1, and solve for d:

`\begin{aligned} p(0) & = 1\\ \implies a(0)^3 + b(0)^2 + c(0) + d & = 1\\ \implies d & = 1 \end{aligned}`

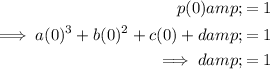
Differentiate the function:

`\begin{aligned} p(x)& = ax^3 + bx^2 + cx + d\\\implies p'(x)&=3 \cdot ax^(3-1)+2 \cdot bx^(2-1)+1 \cdot cx^(1-1)+0 \\p'(x)&=3ax^2+2bx+c\end{aligned}`

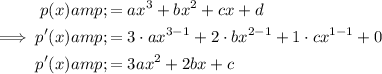
The tangent equation at the point (0, 1) is y = 3x + 1.

Therefore, the gradient of the tangent equation when x = 0 is 3.

To find the gradient of the function at a given point, substitute the x-value of that point into the differentiated function. Therefore, substitute x = 0 into the differentiated function, set it to 3, and solve for c:

`\begin{aligned}p'(0) & =3 \\ \implies 3a(0)^2+2b(0)+c & =3\\ \implies c & = 3\end{aligned}`

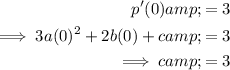
Substitute the found values of c and d into the function:

`p(x) = ax^3 + bx^2 + 3x + 1`

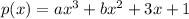
Substitute point (-1, -3) into the function and solve for b:

`\begin{aligned}p(-1) & = -3\\\implies a(-1)^3 + b(-1)^2 + 3(-1) + 1 & = -3\\-a+b-3+1&=-3\\-a+b&=-1\\b&=a-1\end{aligned}`

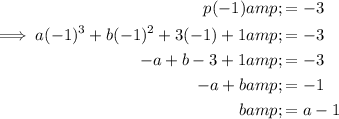
To find the turning points of a function, set the differentiated function to zero and solve for x.

As there is a turning point of function p(x) when x = -1, substitute x = -1 into the differentiated function and set it to zero (remembering to substitute the found value of c = 3 into the differentiated function):

`\begin{aligned} p'(-1) & =0\\\implies 3a(-1)^2+2b(-1)+3 & = 0\\3a-2b+3&=0\end{aligned}`

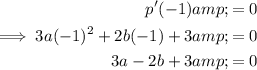
Substitute the found expression for b into the equation and solve for a:

`\begin{aligned}3a-2b+3&=0\\\implies 3a-2(a-1)+3&=0\\3a-2a+2+3&=0\\a+5&=0\\a&=-5\end{aligned}`

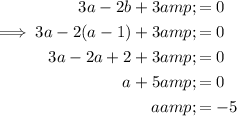
Finally, substitute the found value of a into the found expression for b and solve for b:

`\begin{aligned}b & = a-1\\\implies b & = -5-1\\b & = -6\end{aligned}`

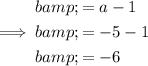
Therefore:

• a = -5
• b = -6
• c = 3
• d = 1

Differentiation Rules

`\boxed{\begin{minipage}{4.8 cm}\underline{Differentiating $ax^n$}\\\\If $y=ax^n$, then $\frac{\text{d}y}{\text{d}x}=nax^(n-1)$\\\end{minipage}}`

`\boxed{\begin{minipage}{4cm}\underline{Differentiating a constant}\\\\If $y=a$, then $\frac{\text{d}y}{\text{d}x}=0$\\\end{minipage}}`