Question

Which graph represent the solution set of this inequality

Answer 1

Hi!

First, let me explain that open circles mean that the answer starts after or before that number. So if the answer is c < 4, the answer would be D, and not B.

If the answer was c ≤ 4, the answer would be B, and not D.

I hope that makes sense. Now let's solve the inequality.

Remember that whatever we do to the inequality, we have to do it to both sides.

We need to isolate c on one side.
10c + 5 ≤ 45
Start by subtracting 5 from both sides.
10c + 5 - 5 ≤ 45 - 5
10c ≤ 40
Divide by 10 on both sides.
10c/10 ≤ 40/10
c ≤ 4

The answer is B.

Hope this helps! :)

Answer 2

Option B is the correct choice.

Explanation:

We have been an inequality
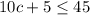`10c+5\leq 45`. We are asked to choose the graph of the solution set of our given inequality.

Let us solve for c:

`10c+5-5\leq 45-5`

`10c\leq 40`

`(10c)/(10)\leq (40)/(10)`

`c\leq 4`

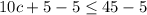
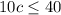
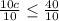
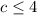
Therefore, the solution of our given inequality is all values of c less than or equal to 4.

Since our given inequality has a less than or equal to sign, so the graph of the solution set would have a solid dot at
`c=4`.

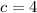Therefore, the graph represented by option B is the correct choice.