Question

What is the measure of angle A in the triangle below? TIMED HELP

Answer 1

The sine of angle-A is 0.5
so the angle is 30 degrees.

Answer 2

Option A is correct

30°

Explanation:

Using sine ratio:

`\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse side}}`

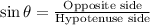
In a given triangle ACB:

BC = 9 units and AB = 18

Opposite side of angle A = BC = 9 units

Hypotenuse side = AB = 18 units.

By sine ratio:

`\sin A = (9)/(18)`

`\sin A = (1)/(2)`

`\sin A = \sin 30^(\circ)`

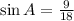
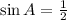
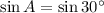
On comparing both sides we have;

`\angle A = 30^(\circ)`

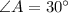
therefore, the measure of angle A is 30 degree.