Question

1. Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary.

B = 74°, a = 14 cm, c = 20 cm


38.59 cm2
134.58 cm2
140 cm2
269.15 cm2

2. Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary.
B = 71°, a = 11 cm, c = 18 cm

99 cm2
32.23 cm2
93.61 cm2
187.21 cm2

3. Given that P = (-5, 5) and Q = (-13, 6), find the component form and magnitude of 2 vector PQ.

<-36, 2>, 2 square root of 325
<16, -2>, square root 65
<-16, 2>, square root of 130
<-16, 2>, square root of two hundred and sixty

Answer 1

1. First, we are going to draw our triangle (picture 1). Next, we are going to use the cosine rule to find the length of side
`b`:

`b^2=a^2+c^2-2accosA`

`b= √(a^2+c^2-2accosA)`

`b= √(14^2+20^2-2(14)(20)cos(74))`

`b=21.02`
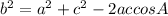
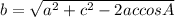
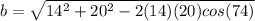
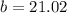
Now that we have all the sides of the triangle, we use Heron's formula to find its area. But first we need to find the semi-perimeter of the triangle. To do it, we are going to use the formula:
`s= (a+b+c)/(2)`
where

`s` is the semi-perimeter.

`a`,
`b`, and
`c` are the sides of the triangle.


`s= (14+21.02+20)/(2)`

`s= (54.02)/(2)`

`s=27.51`

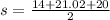
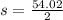
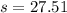
Now, we can use Heron's formula:
`A= √(s(s-a)(s-b)(s-c))`
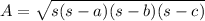
where

`A` is the area of the triangle.

`s` is the semi-perimeter of the triangle.

`a`,
`b`, and
`c` are the sides of the triangle.

`A= √(27.51(27.51-14)(27.51-21.02)(27.51-20)`

`A=134.59cm^2`

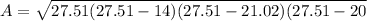
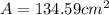
The area of the triangle ABC is 134.59 square centimeters. We can conclude that the correct answer of your given choices is: 134.58 cm2 (your teacher made a little rounding error)

2. Just like before, the first thing we are going to do is draw the triangle (picture 2). Next, we are going to use the cosine rule to find the length of side
`b`:

`b= √(a^2+c^2-2accosA)`

`b= √(11^2+18^2-2(11)(18)cos(71))`

`b=17.78`

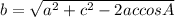
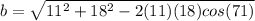
Semi-perimeter:

`s= (a+b+c)/(2)`

`s= (11+17.78+18)/(2)`

`s=23.39`

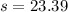
Heron's formula:

`A= √(s(s-a)(s-b)(s-c))`

`A= √(23.39(23.39-11)(23.39-17.78)(23.39-18))`

`A=93.61cm^2`

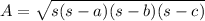
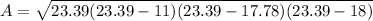
The area of triangle ABC is 93.61 square centimeters. We can conclude that the correct answer is 93.61 cm2

3. We have the vectors P = (-5, 5) and Q = (-13, 6), and we want to find the vector 2 times PQ; in other words, we want to find the result of the multiplication between the vector initiating at P and ending at Q and the scalar 2.
First we are going to find the components of the vector P and ending at Q:

`PQ=\ \textless \ -13-(-5), 6-5\ \textgreater \`

`PQ=\ \textless \ -13+5, 1\ \textgreater \`

`PQ=\ \textless \ -8,1\ \textgreater \`

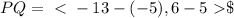
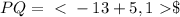
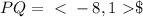
Next, we are going to multiply the vector by the scalar 2:

`2PQ=2\ \textless \ -8,1\ \textgreater \`

`2PQ=\ \textless \ -16,2\ \textgreater \`

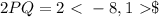
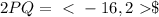
Now, we can find the magnitude of the vector. Remember that the magnitude of a vector is given by the Pythagorean theorem:
`|a|= √(x^2+y^2)`
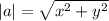
where

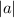`|a|` is the magnitude of the vector

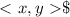`\ \textless \ x,y\ \textgreater \` are the components of the vector.

We know that the components of the vector are
`x=-16` and
`y=2`, so lets replace those vales in our equation:

`|2PQ|= √(-16^2+2^2)`

`|2PQ|= √(-16^2+2^2)`

`|2PQ|= √(256+4)`

`|2PQ|= √(260)`

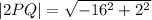
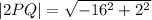
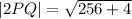
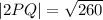
We can conclude that the correct answer is: <-16, 2>, square root of two hundred and sixty.