Answer:
Explanation:
Given: ABC is a triangle.
To prove: BC + AC > BA
Proof: In triangle ABC, we can draw a perpendicular line segment from vertex C to segment AB. The intersection of AB and the perpendicular is called E. We know that BE is the shortest distance from B to CE and AE is the shortest distance from A to CE because of the shortest distance theorem.
Therefore,
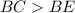 and
and
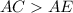 .
.
Now, add the inequalities, we get
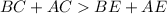 .
.
Then,
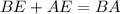 because Segment addition postulate (states that given 2 points E and F, a third point D lies on the line segment EF if and only if the distances between the points satisfy the equation ED + DF = EF)
because Segment addition postulate (states that given 2 points E and F, a third point D lies on the line segment EF if and only if the distances between the points satisfy the equation ED + DF = EF)
Therefore,
 by substitution.
by substitution.