Hey!
To solve x in this equation we must first add five to both sides to get
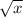
on its own.
Original Equation :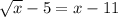 New Equation {Added 5 to Both Sides} :
New Equation {Added 5 to Both Sides} :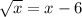
Now we must square both sides of the equation.
Old Equation :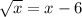 New Equation {Changed by Squaring Both Sides} :
New Equation {Changed by Squaring Both Sides} :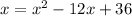
And now we must solve the new equation.
Step 1 - Switch sides
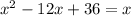
Step 2 - Subtract x from both sides
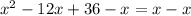
Step 3 - Simplify

Now we need to solve the rest of the equation using the quadratic formula.
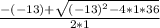
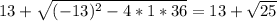
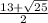
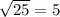
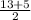

9
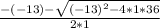
4
So, this means that in the equation
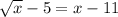 , x = 9 and x = 4.
, x = 9 and x = 4.Hope this helps!
- Lindsey Frazier ♥