Here's your rational expression:
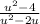
. The numerator of that expression is the difference of perfect squares, and that factors into (u-2)(u+2). In the denominator, you can pull a u out, leaving u(u-2). When you put those factored expressions into its rational form you have
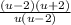
. We have a common term there, u-2 that will cancel out in the numerator and the denominator. When you cross those out, what you're left with is
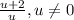
. Hopefully, that is a clear enough explanation.