Question

If dh = 3x -3 and fh = x+7, find the value of x for which defg must be a parallelogram.

a. 7
b. 4
c. 5
d. 2

Answer 1

parallelogram
DH = FH
3x -3 = x + 7
2x = 10
x = 5

Answer
c. 5

Answer 2

Option c is correct

x = 5

Explanation:

Properties of parallelogram:

• Opposites sides are congruent.

• Opposites angle are congruent

• Diagonal of parallelogram bisect each other.

As per the statement:

In the given DEFG parallelogram,

DH = 3x-3 units

FH=x+7 units

by properties of parallelogram we have;

DH = FH

`3x-3 = x+7`

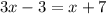
Subtract x from both sides we have;

`2x-3 =7`

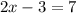
Add 3 to both sides we have;

`2x=10`

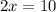
Divide both sides by 2 we have;

x = 5

Therefore, the value of x for which DEFG must be a parallelogram is, 5