Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers. Prove: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. ABCD is a parallelogram.

Answer 1

slope of AD = (2k - 0)/(2j -b - 0) = 2k/(2j - b)
slope of BC = (2k - 0)/(2j - b) = 2k / (2j - b)
AD ║ BC (same slope)

Slope of AB = 0
Slope of DC = 0

AB║DC

Answer 2

`m_(AD)=(2k)/(2j-b)`

`m_(BC)=(2k)/(2j-b)`

`m_(AB)=0`

`m_(DC)=0`

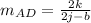
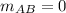
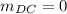
AD║BC

AB║DC

Explanation:

The vertices of parallelogram are A(0,0), B(b,0), C(2j,2k) and D(2j-b,2k).

If a line passes though two points, then the slope of the line is

`m=(y_2-y_1)/(x_2-x_1)`

Using this formula the slope of AD is

`m_(AD)=(2k-0)/(2j-b)=(2k)/(2j-b)`

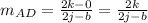
Using the above formula the slope of BC is

`m_(BC)=(2k-0)/(2j-b)=(2k)/(2j-b)`

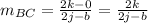
The side AD is parallel to side BC because the slope of two parallel lines are same.

AD║BC

The slope of AB is

`m_(AB)=(0-0)/(b-0)=0`

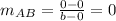
The slope of DC is

`m_(DC)=(2k-2k)/(2j-b-2j)=0`

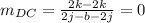
The side AB is parallel to side DC because the slope of two parallel lines are same.

AB║DC

Therefore the required answers are
`m_(AD)=(2k)/(2j-b)`,
`m_(BC)=(2k)/(2j-b)`,
`m_(AB)=0`,
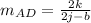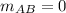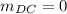`m_(DC)=0`, AD║BC, AB║DC.