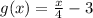Answer:
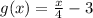
Explanation:
Ve have the function:
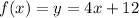
The first step to find the inverse is to exchange the variables, that is where we see
 put
put
 and where we see
and where we see
 put
put
 :
:
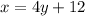
And we clear for the variable
 :
:
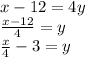
This would be the inverse of the function (since we know that
 ), and according to the problem the inverse of
), and according to the problem the inverse of
 is
is
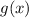 , so:
, so: