Question

Consider the line parameterized by x = 5 − 4t, y = 3 + 8t, z = 10t. find an equation of a plane so that the plane is perpendicular to the line and through the point (2, 5, 1).

Answer 1

2x-4y-5z +21 =0 is the equation.

Explanation:

Given the line can be written as

`(x-5)/(-4) =(y-3)/(8) =(z)/(10)`

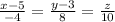
The line has direction ratios (-4, 8, 10)

Since the plane is perpendicular to this line, this line is normal to the plane.

It passes through (2,5,1)

Hence plane will have equation as

-4(x-2)+8(y-5)+10(z-1) =0 Or

-4x+8y+10z +8-40-10 =0

4x-8y-10z +42 =0

Divide by 2

2x-4y-5z +21 =0