Question

What are the two missing sides of the triangle ??

Answer 1

Remark
It's a right triangle so the Pythagorean Theorem applies. All you have to do is put the right things in the right places of the formula.

Givens
a = x
b = x + 4
c = 20

Formula and Substitution.
a^2 + b^2 = c^2
x^2 + (x + 4)^2 = 20^2

Solution
x^2 + x^2 + 8x + 16 = 20 Collect the like terms on the left.
2x^2 + 8x + 16 = 20 Subtract 20 from both sides.
2x^2 + 8x + 16 - 20 = 0
2x^2 + 8x - 4 = 0 Divide through by 2
x^2 + 4x - 2 = 0

Use the quadratic formula
a = 1
b = 4
c = - 2


`\text{x = }\frac{ -b \pm \sqrt{b^(2) - 4ac } }{2a}`

`\text{x = }\frac{ -4 \pm \sqrt{4^(2) + 4(1)(2) } }{2}`

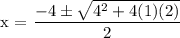
From which x = (-4 +/- sqrt(24) ) / 2
x1 = (- 4 +/- sqrt(4*6) ) / 2
x1 = (- 4 +/- 2 sqrt(6) ) / 2
x1 = -2 + sqrt(6)
x2 = -2 - sqrt(6) This is an extraneous root. No line can be minus.

x1 = + 0.4495
x2 = x + 4 = 4.4495