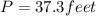By definition the perimeter of an ellipse is given by:
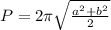
Where,
a: semimajor axis of the ellipse
b: minor semiaxis of the ellipse
Substituting values we have:
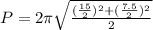
When doing the corresponding calculations, we have that the perimeter is given by:
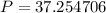
Round to the nearest tenth:
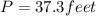 Answer:
Answer:
the estimated perimeter of the ellipse is: