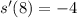Question

The position of an object at time t is given by s(t) = 3 - 4t. Find the instantaneous velocity at t = 8 by finding the derivative.

Answer 1

For this case, we have that the equation of the position is given by:

`s (t) = 3 - 4t`
To find the velocity, we must derive the equation from the position.
We have then:

`s' (t) = - 4`
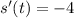
Then, we evaluate the derivative for time t = 8.
We have then:

`s' (8) = - 4`
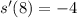Answer:
the instantaneous velocity at t = 8 is:

`s' (8) = - 4`

Answer 2

Answer: - 4


Step-by-step explanation:

As the question tells, the instantaneous velocity is the first derivative of the position.


1) position equation given: s(t) = 3 - 4t

2) derivative, v(t) = s'(t)

s'(t) = [ 3 - 4t]' = (3)' - (4t)' = 0 - 4(t') = - 4

3) Then, the velocity is constant (does not depends on t), and its value is - 4.