Question

A projectile with an initial velocity of 48 feet per second is launched from a building 190 feet tall. The path of the projectile is modeled using the equation h(t) = –16t2 + 48t + 190.Approximately when will the projectile hit the ground?

a. 1.5 secondsB. 3.2 secondsC. 5.3 secondsD. 6.2 seconds

Answer 1

C- 5.3 Seconds

Answer 2

For this case we have the following quadratic equation:

`h (t) = -16t ^ 2 + 48t + 190`
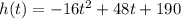
By the time the projectile hits the ground we have the final height equal to zero:

`-16t ^ 2 + 48t + 190 = 0`
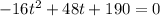
Therefore, we have a second-order polynomial that we must solve:
Using resolver we have:

`x = (-48+/-√(48^2-4(-16)(190)) )/(2(-16))`
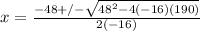
Rewriting:

`x = (-48+/-√(2304+12160) )/(-32)`

`x = (-48+/-√(14464) )/(-32)`
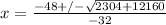
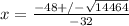
Doing the calculations we have two roots:

`t1 = 5.3 t2 = -2.3`
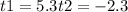
We discard the negative root because we are looking for time which is greater than zero.
Answer:
the projectile will hit the ground after:
C. 5.3 seconds