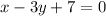Question

What is the equation of a line, in general form that passes through point (1,-2) and had a slope of 1/3

3x-y-7=0
X-3y+7=0
X-3y-7=0

Answer 1

Third option.

Use y = mx + b (slope-intercept form) to get

y = (1/3)x + b.

Then plug in the point (1,-2) for x and y to figure out b...

-2 = (1/3)(1) + b

-2 - 1/3 = b, so b = -7/3

Now you have y = (1/3)x - 7/3. Convert to standard form by multiplying each term by 3 to get

3y = x - 7. Then move the 3y to the other side to get 0 = x - 3y - 7

Answer 2

Answer:
`x-3y+7=0`

Explanation:

The equation of line passing from point (a,b) and has slope m is given by :-

`(y-b)=m(x-a)`

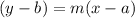
Given : Point = (1,-2)

Slope of line=
`(1)/(3)`

Now, the equation of a line that passes through point (1,-2) and had a slope of
`(1)/(3)` will be :-

`(y-(-2))=(1)/(3)(x-1)\\\\\Rightarrow\ 3(y+2)=x-1\\\\\Rightarrow\ 3y+6=x-1\\\\\Rightarrow\ x-3y+7=0`

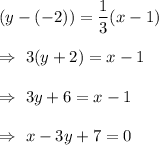
Hence, the equation of a line, in general form that passes through point (1,-2) and had a slope of
`(1)/(3)` is
`x-3y+7=0`