Question

How can we solve this?

Answer 1

Both angles will equal 180, as there is a line bisecting line AB to create the two angles.

Set up the following equation to have both angles equal 180:


`(x + 35) + (x - 23) = 180`


`x + 35 + x - 23 = 180`

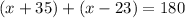
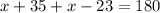
Combine like terms:


`x + x = 2x`

`35 - 23 = 12`


`2x + 12 = 180`

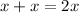
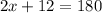
Subtract 12 from both sides:


`2x = 168`

Divide both sides by 2:


`x = 84`

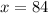
We now know the value of x, so plug it into the equation we set up:


`(84 + 35) + (84 - 23) = 180`


`119 + 61 = 180`

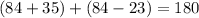
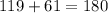
An obtuse angle will have a measure above 90 degrees. The number on the left side that is above 90 degrees is 119. This would be the measure for the obtuse angle.

The obtuse angle is 119 degrees wide.