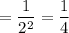To evaluate a number with a negative fraction exponent, you need to take care of two things.
1) The negative exponent.
2) The fraction as an exponent.
1) Negative exponent
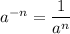
2) Fractional exponent
![a^{(m)/(n)} = \sqrt[n] {a^m} = (\sqrt[n]{a})^m](https://img.qammunity.org/2019/formulas/mathematics/high-school/hpsr97gz6a6b0vnrf4l5dblp5v9gu0jrwc.png)
Example:
Evaluate
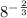
First, take care of the negative exponent.
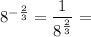
Now we take care of the fractional exponent by using a root.
![= \frac{1}{\sqrt[3] {8^2}} = \frac{1}{(\sqrt[3] {8})^2} =](https://img.qammunity.org/2019/formulas/mathematics/high-school/hatcxojia806jvkghuerovnwr5a9kzdy68.png)