Question

Q 1 Graph the function
Y = |X+2| -3

Answer 1

The graph of y = |x+2| -3 is shown below:

Answer 2

First of all we know the Absolute Value Function that is:


`\left | x \right |= \left \{ {{x \ \ \ \ x \geq 0} \atop {-x \ \ \ \ x\ \textless \ 0}} \right.`

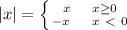
This is called the Parent Function of the Absolute Value Function.

From the equation:


`y=\left | x+2 \right |-3`

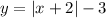
The term:


`\left | x+2 \right |`

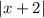
means that the the Parent Function is shifted two units to the left.

On the other hand, the term:


`-3`

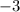
means that the function
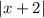
`\left | x+2 \right |` is shifted three units downward. So the result is the graph shown below

Conclusion: The graph is the second one.