Answer: The answers is (A)
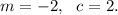 and (B)
and (B)
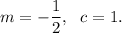
Step-by-step explanation: We are to select the slope and y-intercept of the linear function that is graphed to the left.
We know that the equation of a straight line in slope-intercept form is given by
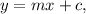
where 'm' is the slope and 'c' is the y-intercept of the line.
Also, a straight line with a positive slope (m>0) rises from left to right whereas a line with a negative slope (m < 0) falls from right to left.
Option (A) is
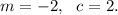
Since 'm' is negative, so the function is graphed to the left.
Option (B) is
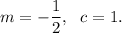
Since 'm' is negative, so the function is graphed to the left.
Option (C) is
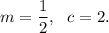
Since 'm' is positive, so the function is graphed to the right.
Option (D) is
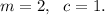
Since 'm' is positive, so the function is graphed to the right.
Thus, (A) and (B) are the correct options.