Question

For which system of equations is (5, 3) the solution? A. 3x – 2y = 9 3x + 2y = 14 B. x – y = –2 4x – 3y = 11 C. –2x – y = –13 x + 2y = –11 D. 2x – y = 7 2x + 7y = 31

Answer 1

The correct answer is:

D)
`\left \{ {{2x-y=7} \atop {2x+7y=31}} \right.`.

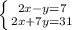
Step-by-step explanation:

We solve each system to find the correct answer.

For A: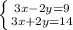

`\left \{ {{3x-2y=9} \atop {3x+2y=14}} \right.`

Since we have the coefficients of both variables the same, we will use elimination to solve this.

Since the coefficients of y are -2 and 2, we can add the equations to solve, since -2+2=0 and cancels the y variable:

`\left \{ {{3x-2y=9} \atop {+(3x+2y=14)}} \right. \\ \\6x=23`

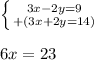
Next we divide both sides by 6:
6x/6 = 23/6
x = 23/6

This is not the x-coordinate of the answer we are looking for, so A is not correct.

For B:

`\left \{ {{x-y=-2} \atop {4x-3y=11}} \right.`

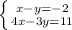
For this equation, it will be easier to isolate a variable and use substitution, since the coefficient of both x and y in the first equation is 1:
x-y=-2

Add y to both sides:
x-y+y=-2+y
x=-2+y

We now substitute this in place of x in the second equation:
4x-3y=11
4(-2+y)-3y=11

Using the distributive property, we have:
4(-2)+4(y)-3y=11
-8+4y-3y=11

Combining like terms, we have:
-8+y=11

Add 8 to each side:
-8+y+8=11+8
y=19

This is not the y-coordinate of the answer we're looking for, so B is not correct.

For C:
Since the coefficient of x in the second equation is 1, we will use substitution again.

x+2y=-11

To isolate x, subtract 2y from each side:
x+2y-2y=-11-2y
x=-11-2y

Now substitute this in place of x in the first equation:
-2x-y=-13
-2(-11-2y)-y=-13

Using the distributive property, we have:
-2(-11)-2(-2y)-y=-13
22+4y-y=-13

Combining like terms:
22+3y=-13

Subtract 22 from each side:
22+3y-22=-13-22
3y=-35

Divide both sides by 3:
3y/3 = -35/3
y = -35/3

This is not the y-coordinate of the answer we're looking for, so C is not correct.

For D:
Since the coefficients of x are the same in each equation, we will use elimination. We have 2x in each equation; to eliminate this, we will subtract, since 2x-2x=0:


`\left \{ {{2x-y=7} \atop {-(2x+7y=31)}} \right. \\ \\-8y=-24`

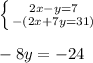
Divide both sides by -8:
-8y/-8 = -24/-8
y=3

The y-coordinate is correct; next we check the x-coordinate Substitute the value for y into the first equation:
2x-y=7
2x-3=7

Add 3 to each side:
2x-3+3=7+3
2x=10

Divide each side by 2:
2x/2=10/2
x=5

This gives us the x- and y-coordinate we need, so D is the correct answer.