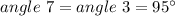We know the following:
The measure of angle 1 is given by this equation:
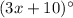
We also know that the measure of angle 4 is as follows:
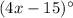
The angles 1 and 4 are
vertically opposite angles. T
he angles opposite each other when two lines cross. They are always equal. Vertical refers to the vertex, where they cross, it does not mean up or down. From this concept it is true that:
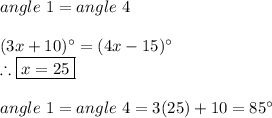
On the other hand, angle 1 and 3 are supplementary, that is, they add up to 180 degrees. So:
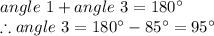
If the lines c and b are parallel, as we can see from the figure, then 3 and 7 are corresponding angles, therefore: