Let t be time and r be rate, then if time varies inversely with the rate, the equation is
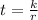
. If it takes 5 hours to drive a fixed distance at a rate of 80, we can sub those values in to solve for the constant of variation, k.

. Solve for k by multiplying 5 and 80 to get that k = 400. Now let's find a new time t when r is a rate of 70. We will use that k value to do this:

and find that it will take 20 hours to drive the distance at 70 mph when it takes 5 hours to drive the distance at 80 mph. Makes sense that it takes longer to drive a fixed distance when you are going slower.