Question

Simplify the rational expression. State any excluded values. 7x-14/x-2

Answer 1

`\bf \cfrac{7x-14}{x-2}\implies \stackrel{common~factoring}{\cfrac{7(x-2)}{x-2}}\implies 7`

well, the only exclusion I can see is that x ≠ 2, because if "x" ever becomes 2, the denominator goes to 0 and the fraction goes poof.

Answer 2

the simplified expression = 7

and the exclude value =2.

Explanation:

The rational expression is
`(7x-14)/(x-2)`

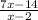
The rational function is undefined id denominator is zero.

Therefore, the excluded value is

x - 2 =0

x = 2

Now, we simplify the expression

Factor out GCF from numerator. The GCF is 7

`(7(x-2))/(x-2)`

Now, cancel out the common term in numerator and denominator

`7`

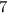
Therefore, the simplified expression is 7 and the exclude value is 2.