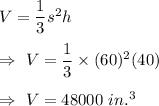Answer: 48000 cubic inches
Explanation:
Given: Slant height of pyramid (l)= 50 in.
Base edge (s)= 60 in.
Let h be the height of the pyramid, the to find the height of the pyramid we consider a portion of pyramid as right triangle, so by Pythagoras theorem we have
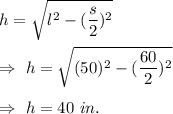
The volume of square pyramid is given by :-