Question

What is the factored form of the polynomial x2 - 16x + 48

Answer 1

(x - 12) (x - 4) is the answer

Answer 2

Answer: The required factored form of the given polynomial is
`(x-4)(x-12).`

Step-by-step explanation: We are given to find the factored form of the following polynomial :

`P(x)=x^2-16x+48.`

To find the factored form, we need to find two numbers whose sum is 16 and product is 48.

The two numbers will be 12 and 4.

The factorization is as follows :

`P(x)\\\\=x^2-16x+48\\\\=x^2-(12+4)x+48\\\\=x^2-12x-4x+48\\\\=x(x-12)-4(x-12)\\\\=(x-4)(x-12).`

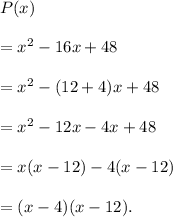
Thus, the required factored form of the given polynomial is
`(x-4)(x-12).`