Question

Please help me find the area of the rhombus

Answer 1

A rhombus is an off-center square. Therefore, all the sides are the same length. Here, they are all 15. Also, the diagonals of a rhombus bisect each other, so if the one segment of the diagonal is 12, then the other half of that segment is also 12. The length of 1 diagonal is 24. We need to find the length of the other side. Using Pythagorean's theorem we can find the leg of that right triangle with side measure 12 and hypotenuse 15.
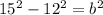
`15^(2)- 12^(2) = b^(2)` and 225 - 144 = b^2, and b^2 = 81 therefore, b = 9. If that half of the segment of the diagonal is 9, then the other half is 9 as well, giving us the second diagonal length of 18. The formula for the area of the rhombus is
`A= (1)/(2) d_(1) d_(2)`.
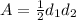
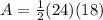
`A= (1)/(2) (24)(18)`. The area, then, is 216 in squared.