Answer:
Explanation:
We are given an equation , so we first need to simplify the equation
lets distribute the x on parenthesis first
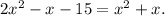
Now bring all terms to the left so we get
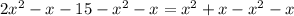
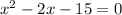
Now since all terms are in one side , so we now factor the equation

Now apply the zero product property to get
x-5=0 or x+3=0
x=5 or x=-3
solution x=-3 or x=5
C